本文共 16833 字,大约阅读时间需要 56 分钟。
堆
堆这种数据结构的应用很广泛,比较常用的就是优先队列。普通的队列就是先进先出,后进后出。优先队列就不太一样,出队顺序和入队顺序没有关系,只和这个队列的优先级相关,比如去医院看病,你来的早不一定是先看你,因为病情严重的病人可能需要优先接受治疗,这就和时间顺序没有必然联系。优先队列最频繁的应用就是操作系统,操作系统的执行是划分成一个一个的时间片的,每一次在时间片里面的执行的任务是选择优先级最高的队列,如果一开始这个优先级是固定的可能就很好选,但是在操作系统里面这个优先级是动态变化的,随着执行变化的,所以每一次如果要变化,就可以使用优先队列来维护,每一次进或者出都动态着在优先队列里面变化。在游戏中也有使用到,比如攻击对象,也是一个优先队列。所以优先队列比较适合处理一些动态变化的问题,当然对于静态的问题也可以求解,比如求解1000个数字的前100位出来,最简单的方法就是排序了,,但是这样多此一举,直接构造一个优先队列,然后出的时候出一百次最大的元素即可。这个时候算法的复杂度就是,如果使用优先队列可以降到
的级别。
| 入队 | 出队 | |
|---|---|---|
| 普通数组 | ||
| 顺序数组 | ||
| 堆 |
现在就要用堆来实现一个优先队列堆一般都是树形结构:
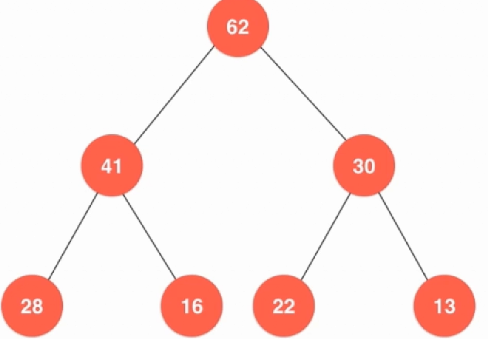
templateclass MaxHeap {private: item *data; int count = 0;public: MaxHeap(int capacity){ data = new item[capacity + 1]; count = 0; } ~MaxHeap(){ delete[] data; } int size(){ return count; } bool isEmpty(){ return count == 0; }};
对于插入一个元素其实也很简单,直接放到最后然后再一步一步的浮上来。新加入的那个元素和他的父亲对比,如果是大于它父亲那么就交换,只到是不大于或者是到了1。因为如果是小于父亲节点那就本身是正确的,如果不终止,再往下比那就是比较其他的元素了,但是其他元素本来就是正确的,所以不需要比较直接结束好了。
void shiftUp(int index) { while (index > 1 && data[index / 2] < data[index]) { swap(data[index / 2], data[index]); index /= 2; } } void insert(item number) { assert(count + 1 <= capacity); data[count + 1] = number; count++; shiftUp(count); } 这样就完成了插入。对于弹出最大的元素就有点边界问题要讨论了。这是一个完全二叉树,所以只有左节点没有右节点,所以首先先要判断是不是有做孩子,也就是越界的问题了,如果没有就继续判断有没有右孩子,有的话就左右孩子比较咯,哪个大就拿哪个出来,在把最大的拿出来和原节点比较即可。这里就需要一个额外的变量了。
void shiftDown(int index) { while (2 * index <= count) { int change = 2 * index; if (change + 1 < count && data[change + 1] > data[change]) { change++; } if (data[change] <= data[index]) { break; } swap(data[change], data[index]); index = change; } } item pop() { assert(count > 0); item target = data[1]; swap(data[1], data[count]); count--; shiftDown(1); return target; } 这样就完成了弹出,弹出的就是最大的数字。事实上这样是可以直接做排序操作的。
现在使用的堆数据结构,是通过不断的交换元素来达到符合堆这个数据结构的目的,但是如果堆里面的元素不是数字,而是字符串或者是很长很长的其他复杂的数据结构,那么交换起来效率就很低,而且这样的话索引起来也有难度。为了解决这些问题,于是就引入了索引堆来解决:
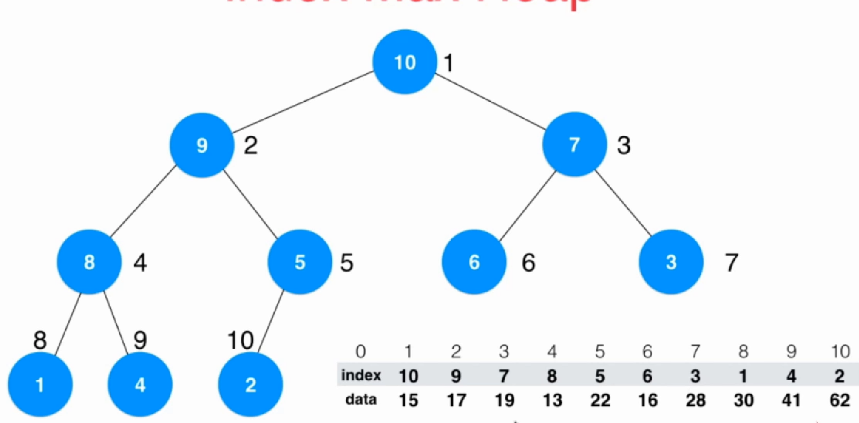
templateclass IndexHeap {private: item *indexes; item *data; int count; int capacity;
shiftDown和shiftUp操作其实就是变一下,把交换的对象换成索引即可:
void shiftUp(int k) { while (k > 1 && data[indexes[k / 2]] < data[indexes[k]]) { swap(indexes[k / 2], indexes[k]); k /= 2; } } void shitDown(int k) { while (2 * k <= count) { int change = 2 * k; if (change + 1 <= count && data[indexes[change]] < data[indexes[change + 1]]) { change++; } if (data[indexes[change]] <= data[indexes[k]]) { break; } swap(indexes[change], indexes[k]); k = change; } } 弹出和插入都是一样的:
void insert(int i, item itemNumber) { assert(count + 1 <= capacity); assert(i + 1 >= 1 && i + 1 < capacity); i++; data[i] = itemNumber; indexes[++count] = i; shiftUp(count); } item extractMax(){ item num = data[indexes[1]]; swap(indexes[1], indexes[count]); count -- ; shitDown(1); return num; } 主要的变化就是对于改变对应索引下的一个元素。改变了之后,我们要知道这个元素的索引是在这个堆的第几个位置才可以进行shift操作,之后还要进行shifDown和shiftUp操作,因为不知道它是可以上浮还是下沉。
void change(int i, item itemNumber){ i += 1; data[i] = itemNumber; for (int j = 1; j <= count; ++j) { if (indexes[j] == i){ shiftUp(j); shitDown(j); return; } } } 但是这个种改变方法最差的情况下是,最后还可以使用一种反向查找的方法进行改进,可以将复杂度提升到
。使用一个reverse数组存储当前索引所在的位置,只有在修改了元素之后就可以直接用
的复杂度从reverse中取出来了。所以有reverse[index[i]] = i,reverse[index]就可以找到当前的元素的位置了。修改代码很简单,reverse和index是绑定在一起的,所以只要index变的地方reverse也要变的。
templateclass IndexMinHeap{private: Item *data; int *indexes; int *reverse; int count; int capacity; void shiftUp( int k ){ while( k > 1 && data[indexes[k/2]] > data[indexes[k]] ){ swap( indexes[k/2] , indexes[k] ); reverse[indexes[k/2]] = k/2; reverse[indexes[k]] = k; k /= 2; } } void shiftDown( int k ){ while( 2*k <= count ){ int j = 2*k; if( j + 1 <= count && data[indexes[j]] > data[indexes[j+1]] ) j += 1; if( data[indexes[k]] <= data[indexes[j]] ) break; swap( indexes[k] , indexes[j] ); reverse[indexes[k]] = k; reverse[indexes[j]] = j; k = j; } }public: IndexMinHeap(int capacity){ data = new Item[capacity+1]; indexes = new int[capacity+1]; reverse = new int[capacity+1]; for( int i = 0 ; i <= capacity ; i ++ ) reverse[i] = 0; count = 0; this->capacity = capacity; } ~IndexMinHeap(){ delete[] data; delete[] indexes; delete[] reverse; } int size(){ return count; } bool isEmpty(){ return count == 0; } void insert(int index, Item item){ assert( count + 1 <= capacity ); assert( index + 1 >= 1 && index + 1 <= capacity ); index += 1; data[index] = item; indexes[count+1] = index; reverse[index] = count+1; count++; shiftUp(count); } Item extractMin(){ assert( count > 0 ); Item ret = data[indexes[1]]; swap( indexes[1] , indexes[count] ); reverse[indexes[count]] = 0; reverse[indexes[1]] = 1; count--; shiftDown(1); return ret; } int extractMinIndex(){ assert( count > 0 ); int ret = indexes[1] - 1; swap( indexes[1] , indexes[count] ); reverse[indexes[count]] = 0; reverse[indexes[1]] = 1; count--; shiftDown(1); return ret; } Item getMin(){ assert( count > 0 ); return data[indexes[1]]; } int getMinIndex(){ assert( count > 0 ); return indexes[1]-1; } bool contain( int index ){ return reverse[index+1] != 0; } Item getItem( int index ){ assert( contain(index) ); return data[index+1]; } void change( int index , Item newItem ){ assert( contain(index) ); index += 1; data[index] = newItem; shiftUp( reverse[index] ); shiftDown( reverse[index] ); }};
堆可以解决的一些问题,首先,就是使用堆来实现优先队列,实现一些选择优先级最高的任务执行。可以作为一些低级工具来实现一些高级数据结构。
Tree
二叉树
二叉树比较常用的地方就是查找了,其实就是类似于二分查找法,把数据分成两份,使用这样的复杂度来进行查找搜索,但是这样就要求这个数组是有序的。比较常用的实现就是查找表的实现。如果使用顺序数组进行查找,使用的复杂度是
,相对应的插入元素也是要
,因为它要遍历所有的元素找到相对应的位置然后插入。但是二分搜索树就更好一些,插入删除查找都是
的复杂度。所以,二分搜索树不仅可以查找数据,还可以高效的插入删除等等,效率很高,适合动态维护数据。而且这种方便的数据结构也可以很好的回答数据关系之间的问题。
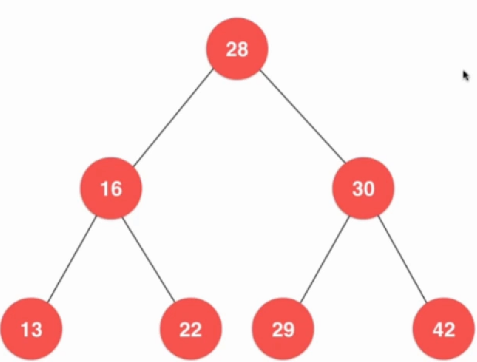
templateclass BST{private: struct Node{ Key key; Value value; Node *left; Node *right; Node(Key key, Value value){ this->key = key; this->value = value; this->left = this->right = NULL; } }; Node *root; int count;public: BST(){ root = NULL; count = 0; } ~BST(){ //TODO } int size(){ return count; } bool isEmpty(){ return count == 0; }};
对于插入其实也很简单。首先和当前根节点比较,如果小于就往左边递归,大于就往右边递归,当当前节点是NULL的时候就到达了递归终点,这个时候已经到头了,new一个新的节点返回当前节点即可。
void insert(Key key, Value value){ root = insert(root, key, value); }private: Node *insert(Node *node, Key key, Value value){ if (node == NULL){ count ++; return new Node(key, value); } if (node->key == key){ node->value = value; } else if(key < node->key){ node->left = insert(node->left, key, value); } else{ node->right = insert(node->right, key, value); } return node; } 二叉树的包含,查找其实都很类似,都是小于往左边找,大于往右边找,只是返回值不一样,操作很常规,比较复杂的是删除操作,要旋转之类的。
Value *search(Node *node, Key key){ if (NULL == node){ return NULL; } else if(node->key == key){ return &(node->value); } else if(key < node->key){ return search(node->left, key); } else{ return search(node->right, key); } } bool contain(Node *node, Key key){ if (NULL == node){ return false; } if (node->key == key){ return true; } else if(key < node->key){ return contain(node->left, key); } else{ return contain(node->right, key); } }}; 以上方法都是放在了私有方法里面的,要调用只需要在public里面加上调用即可:
Value *search(Key key){ return search(root, key); } bool contain(Key key){ return contain(root, key); } 对于search的返回值,其实见仁见智,返回node,固定的一个值都可以。但是如果返回的是一个node,那么调用的时候就需要用户知道程序的结构,比如这道直观node节点是啥才能拿出来,这样封装性就不好了;如果返回的是一个值,那么如果为空的时候就回不来了,所以把它的指针作为返回值。
二叉树的遍历方式有三种,前序遍历,中序遍历和后续遍历。前序遍历先访问当前节点,再访问左右节点;中序遍历先访问左节点,再访问自身,最后右节点;后序遍历先访问左右子树最后才访问自身节点。
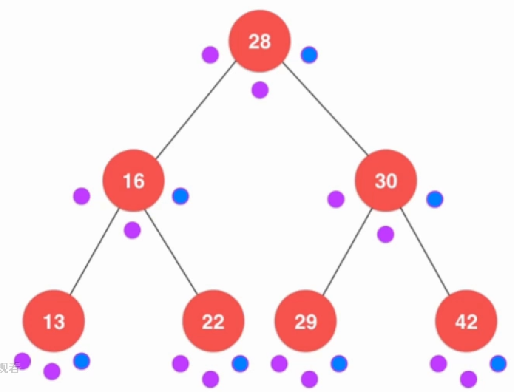
void preOrder(Node *node){ if (node != NULL){ cout << node->value; preOrder(node->left); preOrder(node->right); } } void inOrder(Node *node){ if (node != NULL){ inOrder(node->left); cout << node->value; inOrder(node->right); } } void postOrder(Node * node){ if (node != NULL){ postOrder(node->left); postOrder(node->right); cout << node->value; } } 没有什么难度的。注意到后序遍历是左右才到中间,所以我们可以使用这种方法来对对整棵树进行释放。
void destory(Node *node){ if (node != NULL){ destory(node->left); destory(node->right); delete node; count --; } } 之前我们遍历二叉树都是往深处遍历,都是遍历完一颗子树再遍历其他子树,所以又叫深度遍历。对于遍历方式还有另外一种,就是广度优先遍历,对应到二叉树里面就是层序遍历。先遍历完树的一层再遍历下一层。这种遍历方式没有往深处遍历到底,而是更关注广度的遍历。要实现这种遍历就需要使用到队列,事实上很多广度优先遍历都是用队列来实现,图的广度也是这样实现。
void levelOrder(){ queue q; q.push(root); while (!q.empty()){ Node *p = q.front(); q.pop(); cout << p->value; if (p->left){ q.push(p->left); } if (p->right){ q.push(p->right); } } } 这样很容易就实现了。二叉树的删除操作应该是属于二叉树操作里面比较难的部分,难的不是因为·删除本身,而是在于删除之后要怎么保持树的性质,所以是需要旋转。首先从一个最简单的问题开始,求二叉树最大值和最小值。

Key minimum() { assert(count != 0); Node *node = minimum(root); return node->key; } Key maximum(){ assert(count != 0); Node *node = maximum(root); return node->key; } 最大值和最小值都是一样。删除最小值,删除最小值有两种情况,如果这个最小值刚刚好没有任何节点,删除就很简单,如果是有的话那就需要一些操作了。
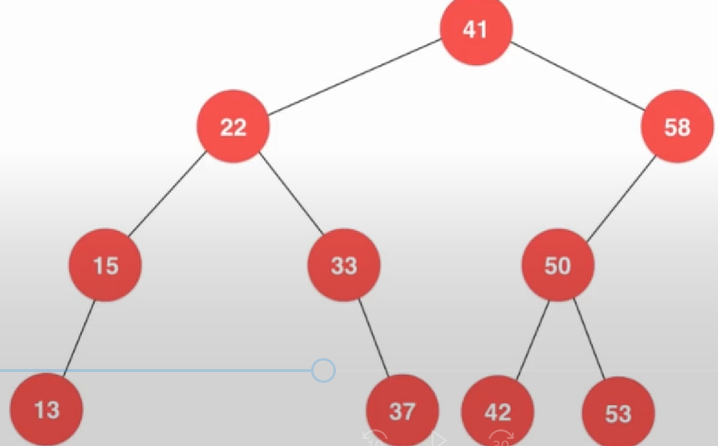
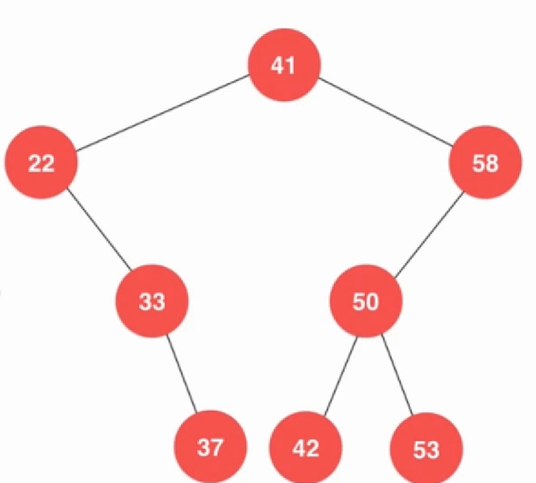
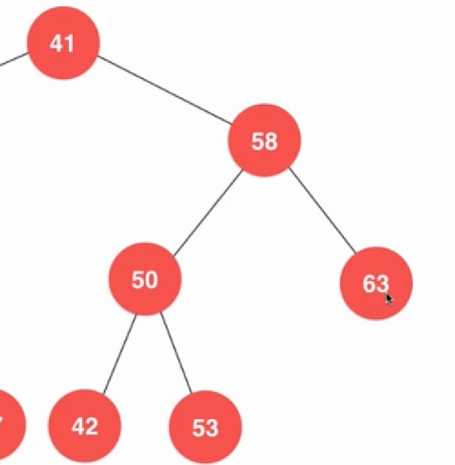
Node *removeMax(Node *node){ if (node->right == NULL){ Node *left = node->left; delete node; count --; return left; } node->right = removeMax(node->right); return node; } Node *removeMin(Node *node){ if (node->left == NULL){ Node *right = node->right; delete node; count --; return right; } node->left = removeMin(node->left); return node; } 其实差不多的。最大值只会有左孩子,最小值只有右孩子。回到删除节点,对于只有右孩子,因为右孩子本来就大于当前节点,只有左孩子也是一样的。最难的就是左右孩子都有的情况,这样就尴尬了:
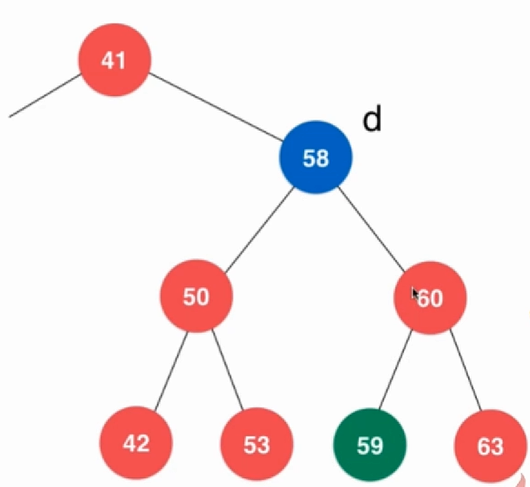
Node *remove(Node *node, Key key){ if ( node == NULL){ return NULL; } else if (key < node->key){ node->left = remove(node->left, key); } else if (key > node->key){ node->right = remove(node->right, key); } else{ if (node->left == NULL){ Node *right = node->right; delete node; count --; return right; } else if (node->right == NULL){ Node *left = node->left; delete node; count --; return left; } else{ Node *delNode = node; Node *successor = new Node(minimum(node->right)); count ++; successor->right = removeMin(node->right); successor->left = node->left; delete delNode; count --; return successor; } } } 首先判断一下是不是只有左子树和右子树,如果只是有一边,那么可以直接把那一边拉上去,如果是两边都有,那就需要找到右边的最小值,代替要删除的节点。这里有一个陷阱,使用successor得到最小的节点之后,后面又删除了,这样就会得到一个空指针,我们只是要得到它并不是要删除,这个时候我们应该要复制一份过来,不能直接就拉过来。
以上的操作都是把二叉树当成一个查找表来实现的,但是二叉树还有一个很好的性质,二叉树是有很好的顺序性,所以二叉树不仅仅可以用来实现查找,还可以找最小值最大值,前驱后继等等。但是二叉树并不是一成不变的,各种元素的插入顺序的不同是可以导致二叉树的结构不一样,如果数据是基本有序的,插入基本就是一个链表的形状了,退化成了一个顺序链表。改进方法后面会提到红黑树AVL树这些更加高级的数据结构。并查集
这个数据结构并不算高级的数据结构,但是在后面的图会用到来判断是否形成环,如果两个节点的根是相同的,那么就可以判断这两个节点是同一组的了,也就是已经连在了一起。之前的堆,二叉树都是树形的结构,而这个并查集也算是一种树形结构,但是和上述的两种不太一样。并查集可以解决的问题有很多,首先就是连接问题:


class unionFind {private: int *id; int count;public: unionFind(int n) { count = n; id = new int(n); for (int i = 0; i < n; ++i) { id[i] = i; } } ~unionFind() { delete[] id; } 一开始大家都是各自为政,没有组团,所以都是不一样的,直接按照序列号即可。查找就是很简单了,就是直接返回id[]即可。
int find(int p) { assert(p >= 0 && p <= count); return id[p]; } 判断是不是连在一起的,直接找到当前属于的下标再比较即可,
void unionElements(int p, int q){ int pID = find(p); int qID = find(q); if (pID == qID){ return; } for (int i = 0; i < count; ++i) { if (id[i] == pID){ id[i] = qID; } } } 连接其实就是把两个堆连在一起,扫描下面的坐标相同的元素赋值即可,赋值那边赋值都可以。这种并查集查找很快,也叫quickUnion。
UF_version1::unionFind uF = UF_version1::unionFind(10); uF.unionElements(1, 2); uF.unionElements(5, 4); uF.unionElements(3, 1); cout << uF.isConnected(4, 5) << endl;
上面这一种实现方法虽然实现查找的时候很快,但是实现并操作的时候很慢,需要进行遍历。并查集的另一种实现方式,而这种实现方式是后面实现并查集的一种常规实现方式。将每一个元素看成是一个节点,如果两个元素是一起的,那么这两个元素是一个指向另一个的。
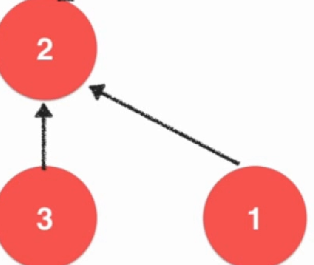
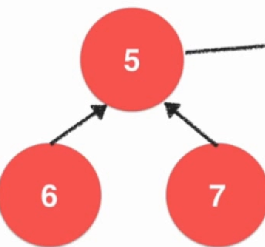
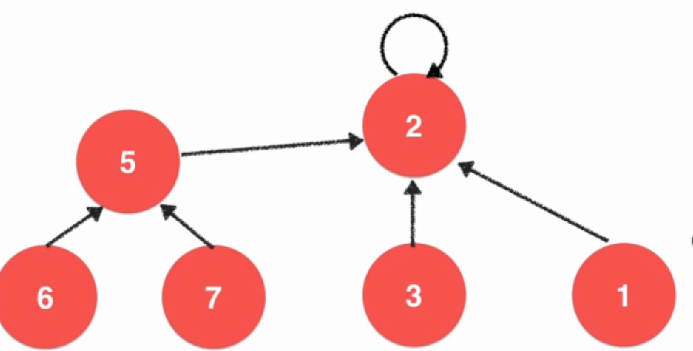
int find(int p){ assert(p >= 0 && p <= count); while (parent[p] != p){ p = parent[p]; } return p; } bool isConnected(int p, int q){ return find(p) == find(q); } void unionElements(int p, int q){ int pRoot = find(p); int qRoot = find(q); if (pRoot == qRoot){ return; } parent[pRoot] = qRoot; } 不断向上找到自己的根,自己等于自己的就是当前的根了,如果不是就向下寻找,直到找到为止。这个时候的合并效率就不低了。注意到代码中的构造函数中有一个ecplicit,因为在c++中单个参数的构造函数是存在有隐式的转换的,加上这个关键字就可以禁止了,只能显示的构造,比如String = "Hello";就是一种隐式构造。
对于这种并查集,还是有优化空间的: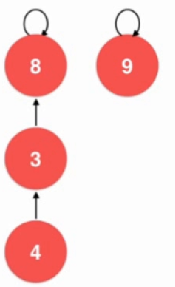
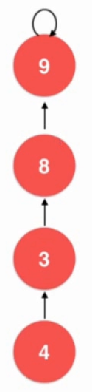
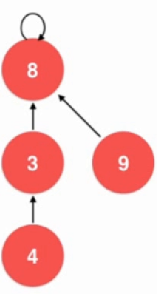
private: int *parent; int *sz; int count;
增加一个sz的数组存储当前这个集合的数量,用于后面插入的比较,哪个大就插哪个。只要改变一下unionElements就好了,其他的不用变。
void unionElements(int p, int q) { int pRoot = find(p); int qRoot = find(q); if (pRoot == qRoot) { return; } if (sz[pRoot] < sz[pRoot]){ parent[pRoot] = qRoot; sz[qRoot] += sz[pRoot]; } else{ parent[qRoot] = pRoot; sz[pRoot] += sz[qRoot]; } } 其实基于数量的优化还不是最优的,如果一个堆过于分散那么合并起来的效率不是很高的,所以还有一种改进方法,就是对比两者的层数插入即可。并查集的线路压缩,以上的插入很多时候有些随机的成分,如果对这个线路的结构进行调整会快很多。这种方法就叫路径压缩。
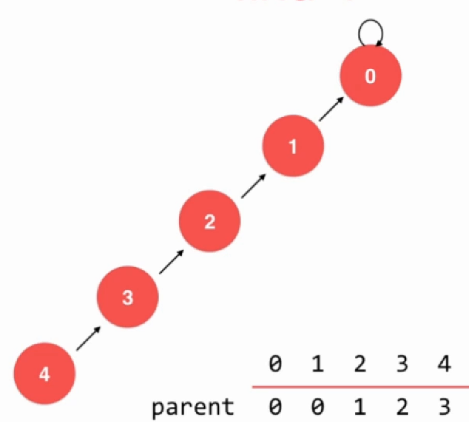
int find(int p) { assert(p >= 0 && p <= count); while (parent[p] != p) { parent[p] = parent[parent[p]]; p = parent[p]; } return p; } 没了,路径压缩就这样。当前节点指向他的根就好了,而find就是找到它的根。递归求解即可。在经过了路径压缩的优化之后查找的复杂度几乎就是复杂度了。
最后附上github地址:
转载地址:http://pavta.baihongyu.com/